Bézier curves in Haskell
I have always been fascinated by the simplicity and versatility of the pen tool in Adobe Illustrator.
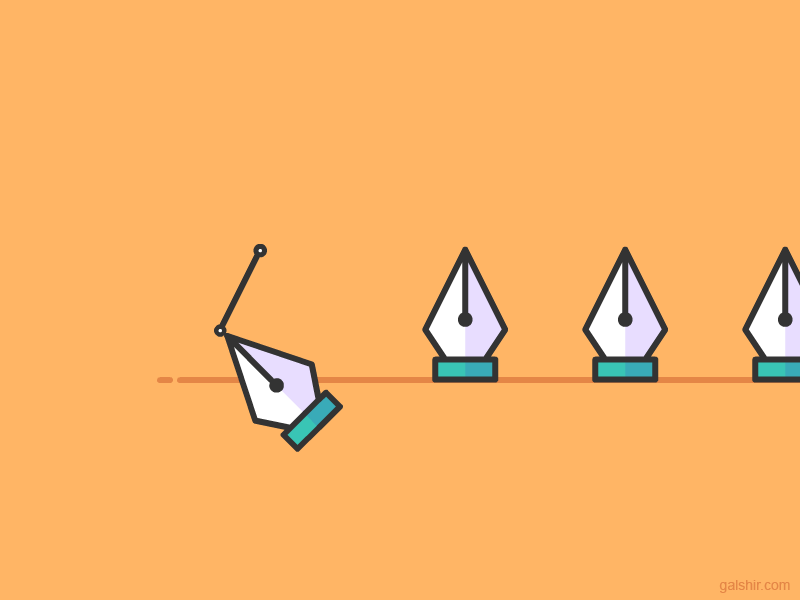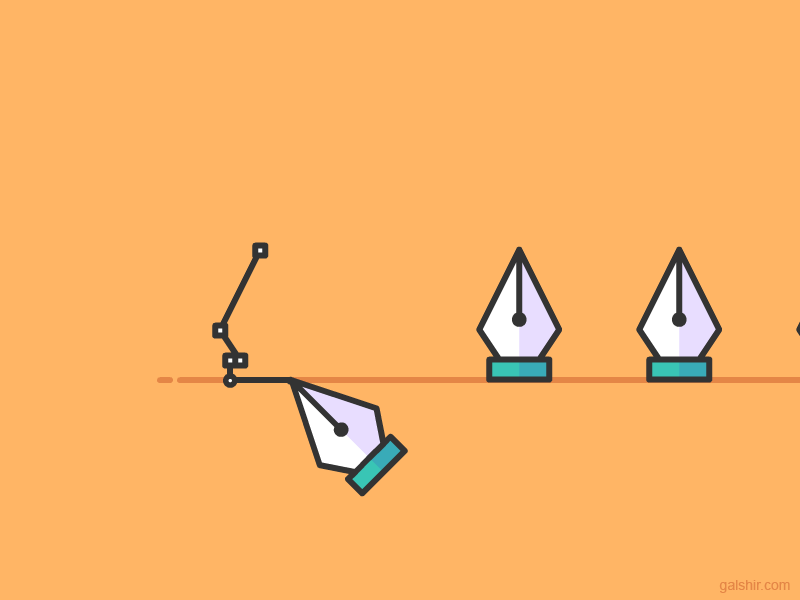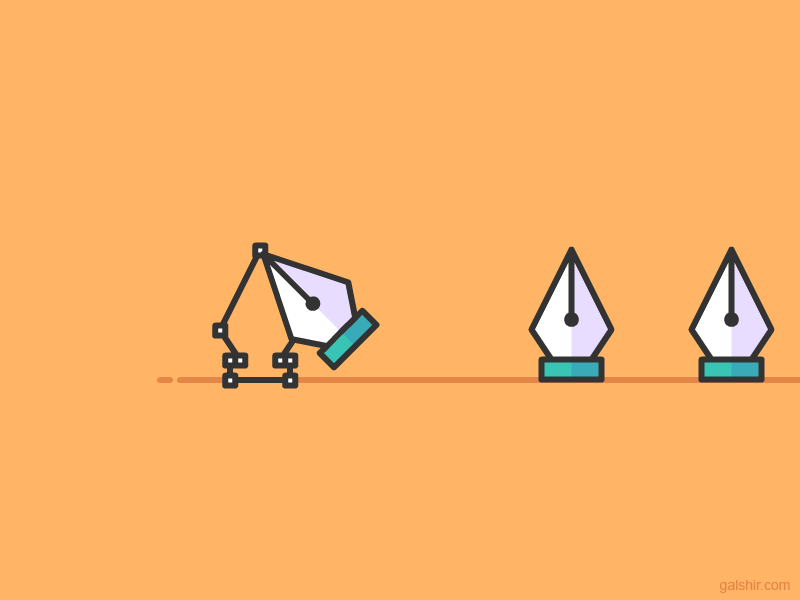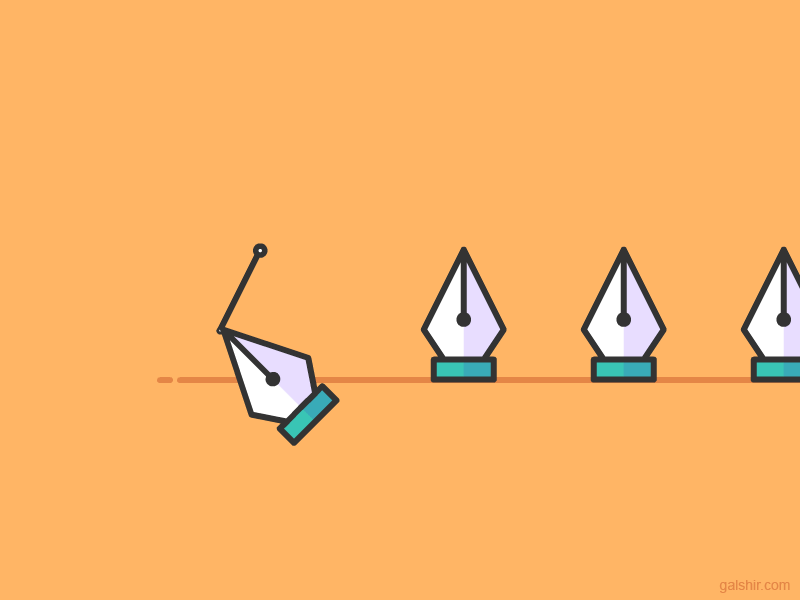
The tool support creation and editing of bézier curves using a simple user interaction. Illustrator support linear, quadratic and cubic bézier curves.
A straight line is a linear bézier curve.

A line with one external point is quadratic bézier curve.
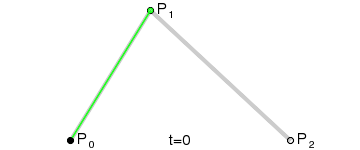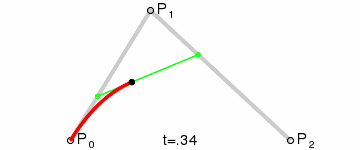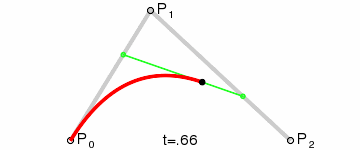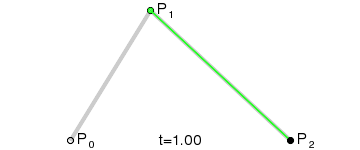
A line with two external points is cubic bézier curve.
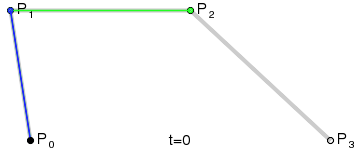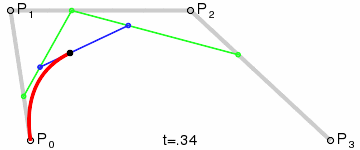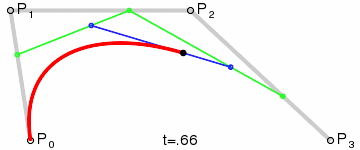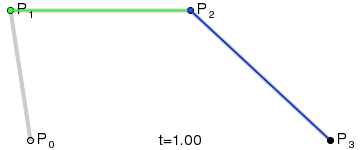
The way Illustrator support creation and editing of bézier curves is to put a handle on each line end point. On a cubic curve one handle is located on point P1 and one on point P2.
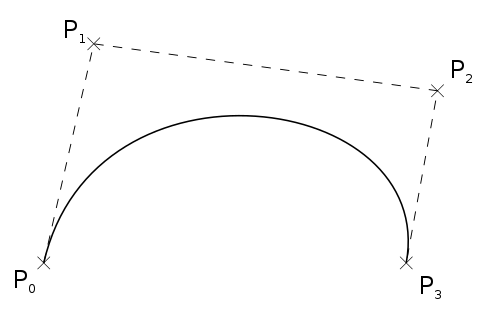
A curve with a single handle represent a quadratic bézier curve and a line with no handles a linear.
Haskell implementation
First I would like to implement bézier curve approximation in Haskell.
The implementation is quite straight forward. The bezier function defines one basic implementation for a linear bézier curve.
Quadratic or higher bézier can be calculated by defining a new set of lines between the bézier points of each line segment and recursively calculating the bézier of that line set, until we only have a single line left. See animations above.
For instance for a cubic bézier you have 3 line segments (P01, P12, P23). Two lines is defined by connecting the bézier points on these three lines which is used to calculate a quadratic bézier. The quadratic bézier can in the same way be reduced to a linear (which we have implemented).
module Main where
import Graphics.Gloss
import qualified Graphics.Gloss.Data.Point.Arithmetic as G
import Graphics.Gloss.Data.Vector
import Prelude hiding (lines)
main :: IO ()
main = do display (InWindow "Bezier" (400, 400) (20, 20)) black $ pic
type Bezier = [Point]
pairs :: [a] -> [(a,a)]
pairs xs = zip xs (drop 1 xs)
-- Generalized higher order Bézier approximation in a single point u [0..1]
bezier :: Bezier -> Float -> Point
bezier (p1:p2:[]) u = p1 G.+ (u G.* (p2 G.- p1)) -- linear
bezier ps u = let ps' = fmap (\(a,b) -> bezier [a,b] u) $ pairs ps -- quadratic or higher
in bezier ps' u
-- Draw approximate Bézier
renderBezier :: Bezier -> Picture
renderBezier b = let len = foldl (\s (a,b) -> s + magV (b G.- a)) 0 $ pairs b
num = floor (len / 5) -- resolution about 5 pixels
steps = fmap ((*) (1/(fromIntegral num)) . fromIntegral) [0..num]
in line $ fmap (bezier b) steps
-- Draw Bézier including control points
showBezier :: Bezier -> Picture
showBezier b = pictures [ Color green $ renderBezier b -- curve
, Color orange $ line [head b, last b] -- linear
, Color (greyN 0.75) $ line b] -- control points
pic :: Picture
pic = Color white
$ showBezier [(0,0),(0,100),(250,200),(200,0)]
The resulting screenshot can be found below.
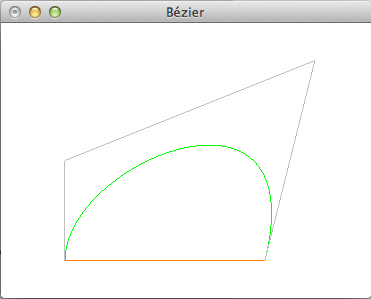
UI for manipulating Bézier curves
The following table summarize a minimal set of actions to allow creation and modification of Bézier curves.
State | Mouse Loc. | Action | Description | New state
----------- | ------------ | ----------------- | ------------------------------ | ---------
Select | Empty space | Click | Start path with (no handles) | Draw
" | Empty space | Click-drag | Start path (handles) | Draw
Draw | Empty space | Click | Add point to path (no handles) | -
" | Empty space | Click-drag | Add point to path (handles) | -
" | - | Escape | Undo last edit | -
Draw/Select | Handle | Click-drag | Modify handles on path [^1] | -
" | Handle | Alt + Click-drag | Modify single handle on path | -
" | Point | Click-drag | Modify point on path | -
Draw | Empty space | Right-Click | Finish path | Select
Select | Point | Alt + Click | Toggle point in selection | -
" | Point | Alt2 + Click-drag | Add handles to point | -
" | Path segmemt | Alt + Click | Toggle path in selection | -
" | Path segmemt | Alt2 + Click | Insert/remove point on path | -
" | Selection | Click-drag | Move selection | -
" | Empty space | Click | Clear selection | -
" | - | Delete | Delete selection | -
[^1]: Handle may be dropped on a point to remove the handle
TODO: Support square select/deselect in Select mode
See dotgrid and ronin for interesting implementations.
References
- Bézier curve (wikipedia)
- Bitmap/Bézier curves/Quadratic (Rosetta Code) - I think its hard to understand the Haskell version and it doesn't seem to be generalized.
